機械学習において学習（最適なパラメータを探すこと）をする際、パラメータ（重さやバイアス）をどちらの方向（減らすのか、増やすのか）に更新するのか決めるのに損失関数（学習で予測した答えと用意した答えの誤差を計算する）というものを参考にします。パラメータを損失関数が少なくなる（正解との誤差が少なくなる）方向に更新するっていうことですね。では、各パラメータの更新する方向を決めるのに具体的にはどうやっているのかということですが、偏微分を使ってそのパラメータが微小に変化したとき損失関数にどれだけ変化を与えるかを求めています。この微小に変化させたとき損失関数が減る方向に微小に変化させる感じです。勾配は、この各パラメータに対する偏微分をまとめたものです。

勾配が消失する理由

まずRNNの計算グラフを見てみます。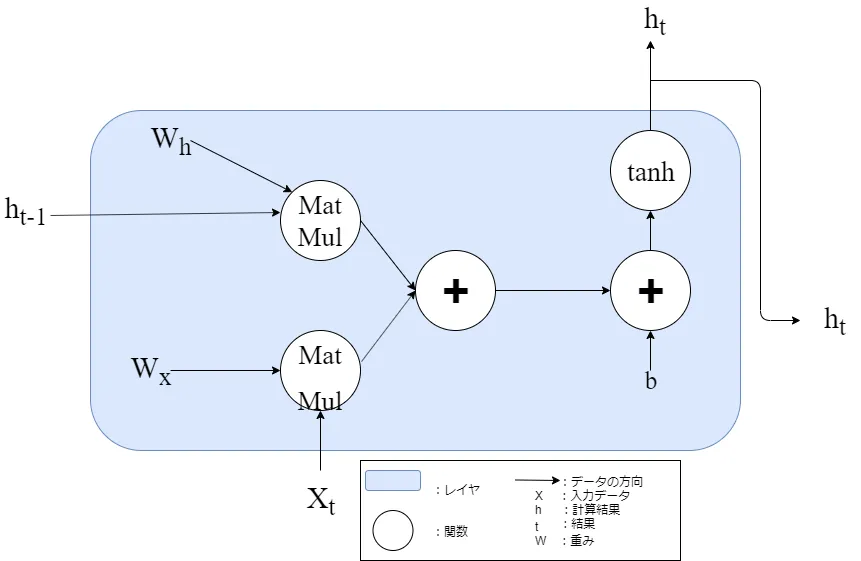図中のMatMulは行列の積、+は行列の和、tanhはハイパボリックタンジェントとします。 RNNを使った人なら見たことある計算グラフですよね。逆伝播時の流れをhに着目してみたときの計算グラフは次のようになります。この逆伝播時に重要になってくるのがtanhです。このtanhが勾配消失の原因になっています。 tanhの微分を見ていくとこの理由がわかります。

$$ \begin{align} y &= tanh(x) = \frac{ e^x - e^{-x} }{ e^x + e^{-x}} \\ y'&= \Bigl( \frac{ e^x - e^{-x} }{ e^x + e^{-x}} \Bigr)' \\ &=\frac{ (e^x + e^{-x})^2 - (e^x - e^{-x})^2 }{ (e^x + e^{-x})^2}\\ &=\frac{ 4 }{ (e^x + e^{-x})^2}\\ \end{align} $$

ここで微分が終わっていますがのちの説明をしやすくするため変形していきます。

$$ \begin{align} &=\frac{1}{\Bigl(\frac{e^x+e^{-x}}{2}\Bigr)^2}\\ &=\frac{1}{cosh^2x}\\ &=\frac{cosh^2x-cosh^2x+1}{cosh^2x}\\ &=1-\frac{cosh^2x-1}{cosh^2x}\\ &=1-\frac{sinh^2x}{cosh^2x}\\ &=1-tanh^2x\\ &=1-y^2 \end{align} $$

yは順伝播時のtanhの出力が入ってきます。これを逆伝播時に流れてくる勾配にかけていきます。つまり時間を経るたび1より小さい数が乗算されていくため、勾配がだんだんと小さくなっていき消失してしまうわけです。

爆発の原因

先ほどの図をもう一度見てみましょう。 +の逆伝搬はただデータを流すだけなので、爆発の原因は行列の積MatMulにありそうです。行列の積の逆伝播は自分とはほかのノードの値を乗算するので、次のようになります。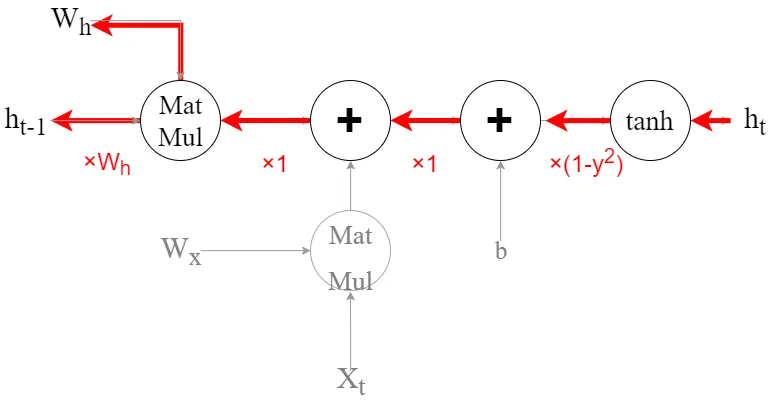見てわかる通り重みWをかけていくので、時間がたつにつれて勾配がどんどん大きくなってしまいます。これが勾配が爆発する理由です。

おわりに

とりあえず、自分が腑に落ちた理解がこのような感じです。間違えていたり、もっとわかりやすい考え方あるよと思った方是非教えてください。

勾配消失・爆発

目次